CARbon MAnifolds

Finding the isometric embedding guaranteed by Alexandrov's theorem in a robust way is presently an unsolved problem: the state-of-the-art uses numerical force-field optimization (Brinkmann et al. 2010, Schwerdtfeger et al. 2013, Wirz et al. 2015), which often works, but it is prone to failure if the initial guess is far from the correct shape, and it breaks down more often as fullerenes grow in size.

This task will start from my recent work presented here. The central idea is as follows: For fullerenes, the positions of the pentagons uniquely determine the fullerene's shape. The idea explored here is to thin out the graph in a certain metric-preserving way by maintaining a Delaunay-triangulation, and to use the surface metric to find the coarse polyhedron defined by the 12 pentagon vertices. The 12-vertex polyhedron can then be embedded in a robust way (and uniquely, by Alexandrov) due to the fixed vertex count.

(a)	(b)

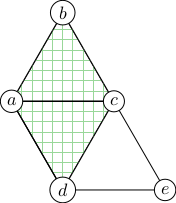
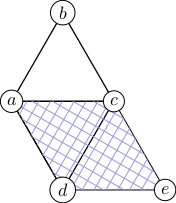
Computing the Delaunay triangulation is made difficult by the fact that it isn't possible to make a single two-dimensional coordinate system for the whole fullerene surface. However, it is possible to make overlapping patches of flat coordinate systems. In particular, any two adjacent triangles share a coordinate system, and this can be extended to regions that contain no Gaussian curvature. Inside such regions, angles and lengths can be worked out as in Cartesian coordinates, but anything that goes outside of the ``safe'' region potentially yields nonsense. The information used in the Delaunay triangulation algorithm has to, in each step, remain within the progressively growing flat regions.

1. Isometric coarsening of point-set to only cone points.
2. Unfolding/folding Delaunay triangulation to Eisenstein polygons.
3. 3D embedding of coarse metric. Preliminary experiments yielded a coarse shape, which can be used for shape classification and search, in milliseconds.
4. Full 3D embedding derived from coarse embedding. Preliminary experiments yielded 3D geometry very near to full DFT/B3LYP optimized geometry in tens of seconds.

Preliminary Work:

• In Intrinsic Geometries of Fullerenes, I presented a partial prototype of this idea, but in which the Delaunay-step had to be hand annotated. The figure above shows the steps of a test calculation for a barrel-shaped $C_{480}$. The coarse and interpolated shapes were calculated in miliseconds. Similar timing was obtained for $C_{3000}$. However, more work is still necessary for creating a robust, efficient solution.
• MSc Thesis: Buster Pedersen, Shapes of Fullerenes: Fast, Parallel Molecular Geometry. A master's student thesis is under way that builds numerical codes for finding molecular 3D geometry from surface metrics for entire isomer spaces at a time (millions of molecular structures in parallel on GPU). The challenge is that optimization either must always succeed, or always detect failure, as millions of structures cannot be inspected by hand.